
In the Schrödinger picture, states evolve according to the Schrödinger equation
(1) ![]()
where ![]() is the Hamiltonian of the system (and
is the Hamiltonian of the system (and ![]() ). Because the Hamiltonian is a hermitian operator, one can define a unitary evolution operator
). Because the Hamiltonian is a hermitian operator, one can define a unitary evolution operator ![]() which takes
which takes ![]() to
to ![]() for all states. The evolution operator obeys the differential equation
for all states. The evolution operator obeys the differential equation
![]()
Simple case
If ![]() is constant, then the differential equation is easy, and the evolution operator can be written
is constant, then the differential equation is easy, and the evolution operator can be written
![]()
If ![]() does depend on time, but at least commutes with itself across different times, then
does depend on time, but at least commutes with itself across different times, then ![]() can be generalized to
can be generalized to
![]()
General case
If we have no such guarantees on ![]() , then things get more interesting. We can integrate the Schrödinger equation
, then things get more interesting. We can integrate the Schrödinger equation
![Rendered by QuickLaTeX.com \[\ket{\psi(t)}=\ket{\psi(t')}-i\int_{t'}^t dt_0\hat{H}(x,p,t_0)\ket{\psi(t_0)}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-29b6cb5145844b02a39f91a11e13988e_l3.png)
And then iterate by expanding the ![]() part:
part:
(2) 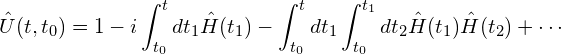
This gives us an infinite sum of integrals to evaluate to find ![]() . But we can play some games to make it prettier. We could for instance take the second-order term in that expansion and extend the upper limit of the inner integral to
. But we can play some games to make it prettier. We could for instance take the second-order term in that expansion and extend the upper limit of the inner integral to ![]() provided we insert a
provided we insert a ![]() to kill off the
to kill off the ![]() region.
region.
![Rendered by QuickLaTeX.com \[\text{second-order term}=-\int_{t_0}^t dt_1\int_{t_0}^{t}dt_2\theta(t_1-t_2)\hat{H}(t_1)\hat{H}(t_2)\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-b1c8b9106c66121a8d7cc9c1366d548c_l3.png)
Or further, we could recognize that the integral in the ![]() region is the same as the integral in the
region is the same as the integral in the ![]() region but with the operators flipped. So let’s allow both regions but divide by two.
region but with the operators flipped. So let’s allow both regions but divide by two.
![Rendered by QuickLaTeX.com \begin{align*} \text{second-order term}&=\frac{-1}{2}\left\{ \int_{t_0}^t dt_1\int_{t_0}^{t}dt_2\theta(t_1-t_2)\hat{H}(t_1)\hat{H}(t_2)+ \int_{t_0}^t dt_1\int_{t_0}^{t}dt_2\theta(t_2-t_1)\hat{H}(t_2)\hat{H}(t_1) \right\}\\ &=\frac{-1}{2} \int_{t_0}^t dt_1\int_{t_0}^{t}dt_2\mathcal{T}\left[\hat{H}(t_1)\hat{H}(t_2)\right]\\ &=\mathcal{T}\left[\frac{-1}{2} \left(\int_{t_0}^t dt_1\hat{H}(t_1)\right)^2\right] \end{align*}](https://sambader.net/wp-content/ql-cache/quicklatex.com-87bc5264ce1e56510666a23755f92216_l3.png)
where ![]() is the time-ordering “operation”: it just rearranges the operators inside its brackets to be ordered latest-on-the-left without any regard for whether those operators commute.
is the time-ordering “operation”: it just rearranges the operators inside its brackets to be ordered latest-on-the-left without any regard for whether those operators commute.
We can do this funny business for every term of the expansion 2: for the ![]() -th term, extend all the
-th term, extend all the ![]() limits of integration, put in the time-ordering operator, and divide by the
limits of integration, put in the time-ordering operator, and divide by the ![]() permutations of the operators. We find
permutations of the operators. We find
(3) 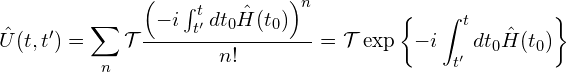
where the last equality is just a definition. This is known as the Dyson series.
Double-check
We can “check ourselves” that this is valid. Since ![]() rearranges operators freely, anything inside a
rearranges operators freely, anything inside a ![]() effectively commutes. So we can treat everything like numbers when we differentiate by
effectively commutes. So we can treat everything like numbers when we differentiate by ![]() .
.
![Rendered by QuickLaTeX.com \[\frac{d}{dt}\hat{U}(t,t')=\mathcal{T}\left[-i\hat{H}(t)\exp\left\{-i\int_{t'}^{t}dt_0\hat{H}(t_0)\right\}\right]=-i\hat{H}(t)\mathcal{T}\left[\exp\left\{-i\int_{t'}^{t}dt_0\hat{H}(t_0)\right\}\right]=-i\hat{H}(t)\hat{U}(t,t')\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-af9d805c8ad359bbecfb761ffe8919ed_l3.png)
where, in the middle equality, we can pull ![]() out of the
out of the ![]() on the left because
on the left because ![]() is the latest time.
is the latest time.