
Suppose we have a Hamiltonian
![]()
where ![]() is the solvable (“free”) part and
is the solvable (“free”) part and ![]() is the “interaction” term. The Gell-Mann theorem gives us a (non-perturbative) expression for the eigenstates of
is the “interaction” term. The Gell-Mann theorem gives us a (non-perturbative) expression for the eigenstates of ![]() by adiabatically switching off the interaction term, and evolving an eigenstate from where the Hamiltonian is free to where it is interacting.
by adiabatically switching off the interaction term, and evolving an eigenstate from where the Hamiltonian is free to where it is interacting.
The beginning of this post will mainly follow Molinari. We will consider the related Hamiltonian
![]()
, which has the interaction turned off at ![]() . So, in the interaction picture, the system should adiabatically approach a constant state at
. So, in the interaction picture, the system should adiabatically approach a constant state at ![]() .
.
The answer in advance:
Our adiabatic intuition suggests that we should have interaction picture eigenstates ![]() , where
, where ![]() is an eigenstate of
is an eigenstate of ![]() with energy
with energy ![]() . Unfortunately, as we take an adiabatic limit
. Unfortunately, as we take an adiabatic limit ![]() ,
, ![]() is undefined because the interaction time keeps expanding, rotating the phase of
is undefined because the interaction time keeps expanding, rotating the phase of ![]() around and around (the phase goes as
around and around (the phase goes as ![]() ). Operators such as
). Operators such as ![]() are known as Møller operators, and their weird properties (such as not actually being unitary!) are well-studied (see Chapter 9 of Kleinert).
are known as Møller operators, and their weird properties (such as not actually being unitary!) are well-studied (see Chapter 9 of Kleinert).
We can cancel out this ill-defined phase though: divide by a matrix element which also picks up the phase before we take the ![]() limit. We will show below that the following approaches an eigenstate of the full interacting Hamiltonian in that adiabatic limit:
limit. We will show below that the following approaches an eigenstate of the full interacting Hamiltonian in that adiabatic limit:
(1) 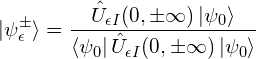
(assuming the limit exists!)
First, we just need one lemma:
We are interested in the evolution operator ![]() and how it depends on the interaction strength
and how it depends on the interaction strength ![]() . For computational convenience (because of the absolute value in our
. For computational convenience (because of the absolute value in our ![]() ), we will only care about when
), we will only care about when ![]() and
and ![]() have the same sign (and this will be all we need).
have the same sign (and this will be all we need).
First, rewrite ![]() as
as ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \hat{H}_\epsilon(t)= \begin{cases} \hat{H}_0+e^{-\epsilon (t-\theta)}g\hat{V}, & t \ge 0\\ \hat{H}_0+e^{\epsilon (t+\theta)}g\hat{V}, & t \le 0 \end{cases} \]](https://sambader.net/wp-content/ql-cache/quicklatex.com-e37457ff0b27c50613da9ea65ed3b9c7_l3.png)
This shows us that putting in an interaction whose strength is described by ![]() is the same as translating the Hamiltonian backwards (forwards) in time by
is the same as translating the Hamiltonian backwards (forwards) in time by ![]() if
if ![]() (
(![]() ). Since the effect of
). Since the effect of ![]() is just a time-shift, we can easily work out how the (Schrodinger picture) evolution operator changes with
is just a time-shift, we can easily work out how the (Schrodinger picture) evolution operator changes with ![]() :
:
![]()
Using ![]() , we can transfer this to the interaction picture where we will work for the rest of the proof:
, we can transfer this to the interaction picture where we will work for the rest of the proof:
![]()
where ![]() . Using
. Using ![]() and
and ![]() , and
, and ![]() , we find
, we find
![]()
Plugging in ![]() and
and ![]() :
:
![]()
Now if we apply this to an eigenstate ![]() of
of ![]() with energy
with energy ![]() , we find (noting
, we find (noting ![]() and
and ![]() ):
):
(2) ![]()
This handy formula connects the dependence of the evolution operator on the interaction to how the interaction part of the Hamiltonian acts on our state of interest.
Showing that our answer is correct:
If we differentiate our answer 1 with respect to ![]() and use our lemma 2 to simplify the derivatives
and use our lemma 2 to simplify the derivatives
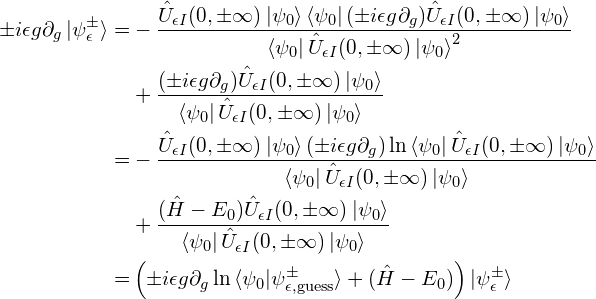
Now if we take the ![]() limit, the term on the left of the equality vanishes (because our answer state is a well-behaved ket). This shows that
limit, the term on the left of the equality vanishes (because our answer state is a well-behaved ket). This shows that ![]() is an eigenstate of the full Hamiltonian with energy
is an eigenstate of the full Hamiltonian with energy
(3) ![]()
(Note that the energy shift ![]() does NOT vanish in the limit, because the phase of our “guess” state goes as
does NOT vanish in the limit, because the phase of our “guess” state goes as ![]() , countering the
, countering the ![]() prefactor.) There we have it: the Gell-Mann and Low Theorem.
prefactor.) There we have it: the Gell-Mann and Low Theorem.
Note also that Gell-Mann and Low don’t exclude level crossing: if ![]() is the ground state, then
is the ground state, then ![]() might not be. The
might not be. The ![]() state and
state and ![]() state are adiabatically connected, but, if there’s an accidental degeneracy along the path from
state are adiabatically connected, but, if there’s an accidental degeneracy along the path from ![]() to
to ![]() then we might enter some excited state along the evolution. Let us for now exclude that possibility (eg make
then we might enter some excited state along the evolution. Let us for now exclude that possibility (eg make ![]() too small to upset the order of the low-energy
too small to upset the order of the low-energy ![]() eigenstates). In this case, we can say that the two eigenstates we’ve found are precisely the same, since they are adiabatically connected and the Hamiltonian is the same at
eigenstates). In this case, we can say that the two eigenstates we’ve found are precisely the same, since they are adiabatically connected and the Hamiltonian is the same at ![]() .
.
Use in QFT:
The Gell-Mann and Low theorem leads to a wonderful rewriting of Green’s functions in Quantum Field Theory. We have by definition
![]()
where ![]() is the full interacting ground state. If we plug in our expression for the ground state 1 in the interaction picture (remembering to normalize it!), and do a bit of playing around*, we can write our answer as
is the full interacting ground state. If we plug in our expression for the ground state 1 in the interaction picture (remembering to normalize it!), and do a bit of playing around*, we can write our answer as
![Rendered by QuickLaTeX.com \[G^{(n)}(x_1,\cdots, x_n)=\frac{\bra{0}\mathcal{T}\phi_{1}(x_1)\cdots\phi_{n}(x_n)S\ket{0}} {\braket{0|S|0}}}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-56755230088095c4919103b72c92145d_l3.png)
Anyway, the expression on the right is something we know how to evaluate, since it involves only the free ground state. If we work in the interaction picture, then the we can do mode expansions of the operators (and a Dyson series for ![]() ), then use Wick’s theorem to grind the Green’s function down. (We couldn’t do mode expansions of the Heisenberg operators since they don’t obey a simple wave equation like the interaction picture operators do.) And that’s how Green’s functions become just another exercise in Feynman diagrams!
), then use Wick’s theorem to grind the Green’s function down. (We couldn’t do mode expansions of the Heisenberg operators since they don’t obey a simple wave equation like the interaction picture operators do.) And that’s how Green’s functions become just another exercise in Feynman diagrams!
* You can find the steps shown in Yeh’s “Advanced Condensed Matter Field Theory”. But there’s actually a great deal of subtlety involved in the “playing around” part of this concerning how ![]() is defined. It confused me for a while, and I ended up asking and then answering for myself a question about it on Physics Stack Exchange. I put a lot of thought into explaining this actually works, so, if you enjoyed the Gell-Mann Low theorem and want to really understand the intermediate steps to the last expression here, I suggest you check it out.
is defined. It confused me for a while, and I ended up asking and then answering for myself a question about it on Physics Stack Exchange. I put a lot of thought into explaining this actually works, so, if you enjoyed the Gell-Mann Low theorem and want to really understand the intermediate steps to the last expression here, I suggest you check it out.