
There are three major “pictures” of Quantum Mechanics which are simply different ways of assigning the time-dependence among the state vectors versus the operators, and I just want a quick reference on how everything evolves in every picture.
Schrödinger Picture
The Schrödinger picture is the canonical way of describing quantum mechanics. The operators such as ![]() and
and ![]() are time-independent. Some operators may have an explicit time-dependence, but this dependence reflects external changes, eg modelling an atom in a time-changing electric field, not the natural evolution of the system itself.
are time-independent. Some operators may have an explicit time-dependence, but this dependence reflects external changes, eg modelling an atom in a time-changing electric field, not the natural evolution of the system itself.
So Schrödinger operators ![]() don’t change in time (unless explicitly changed), but state vectors do evolve, according to the Schrödinger equation:
don’t change in time (unless explicitly changed), but state vectors do evolve, according to the Schrödinger equation:
(1) ![]()
The evolution operator going from ![]() to
to ![]() is
is
![Rendered by QuickLaTeX.com \[\hat{U}(t, t')=\mathcal{T}\exp\left\{-i\int_{t'}^{t}dt_0\hat{H}(t_0)\right\}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-d73525f86b00cb0b3f36e6437d817db4_l3.png)
as shown in a prior note. Or, if ![]() is constant,
is constant,
![]()
Heisenberg Picture
The Heisenberg picture transfers all of the the time-dependence into the operators, so the states become constant kets. By convention, we set the Heisenberg kets equal to the zero-time Schrödinger kets:
![]()
In order to produce the same physical predictions, all inner products must be the same as in the Schrödinger picture, so this requires
![]()
where ![]() is exactly what was found for the Schrödinger picture. Or, differentially, we have
is exactly what was found for the Schrödinger picture. Or, differentially, we have
![Rendered by QuickLaTeX.com \[i\frac{d}{dt}\hat{O}_H(t)=[\hat{O}_H(t),\hat{H}(t)]+U^{\dagger}(t,0)i\frac{d\hat{O}_S(t)}{dt}U(t,0)\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-1e303f739f9c1c62a8d7c866a82daa7b_l3.png)
So, if the operator has no explicit time dependence, it only evolves by its commutator with the Hamiltonian.
Interaction picture
The interaction picture breaks up the Hamiltonian into a “free” (or solvable) part ![]() , and an “interacting” (or unsolvable) part
, and an “interacting” (or unsolvable) part ![]() . The operators pick up the part of the evolution due to the free part. That is to say the operators are defined to evolve as in the Heisenberg picture of the Hamiltonian
. The operators pick up the part of the evolution due to the free part. That is to say the operators are defined to evolve as in the Heisenberg picture of the Hamiltonian ![]() :
:
![]()
with
![Rendered by QuickLaTeX.com \[\hat{U}_0(t, t')=\mathcal{T}\exp\left\{-i\int_{t'}^{t}dt_0\hat{H_0}(t_0)\right\}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-58cabb070fc8a5efbfa484f411a23cf0_l3.png)
and that part of the evolution is cancelled from the states:
![]()
In order to preserve inner products, the evolution operator for the interaction picture states must then be
![]()
where ![]() is the full evolution operator,
is the full evolution operator,
![Rendered by QuickLaTeX.com \[\hat{U}(t, t')=\mathcal{T}\exp\left\{-i\int_{t'}^{t}dt_0\hat{H}(t_0)\right\}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-d73525f86b00cb0b3f36e6437d817db4_l3.png)
We differentiate to find that
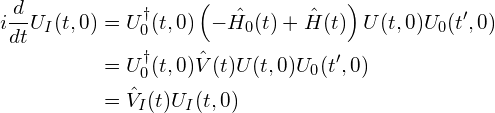
where ![]() . But we know this differential equation:
. But we know this differential equation:
![Rendered by QuickLaTeX.com \[\hat{U}_I(t, t')=\mathcal{T}\exp\left\{-i\int_{t'}^{t}dt_0\hat{V_I}(t_0)\right\}\]](https://sambader.net/wp-content/ql-cache/quicklatex.com-e8844b62dd03f9ceee8fd3f47178c552_l3.png)
The beauty of this picture is that the interaction kets have only the interesting evolution in them, the “transitions” between what would be considered eigenstates of the free Hamiltonian. This intuition of the picture is what leads to the S-Matrix formalism. The interaction picture operators, on the other hand, are pleasantly dull, and just evolve with the free Hamiltonian. (Later, this will be convenient because it lets us use the machinery of mode expansions and Wick’s theorem!)