
To help with an internship project, I wanted to model the frequencies of some transitions in a flux qubit. Long story short, I enjoyed this quick calculation and ended up producing a full numerical solver for bound states in a Time-Independent Schrodinger Equation using NumPy/SciPy.
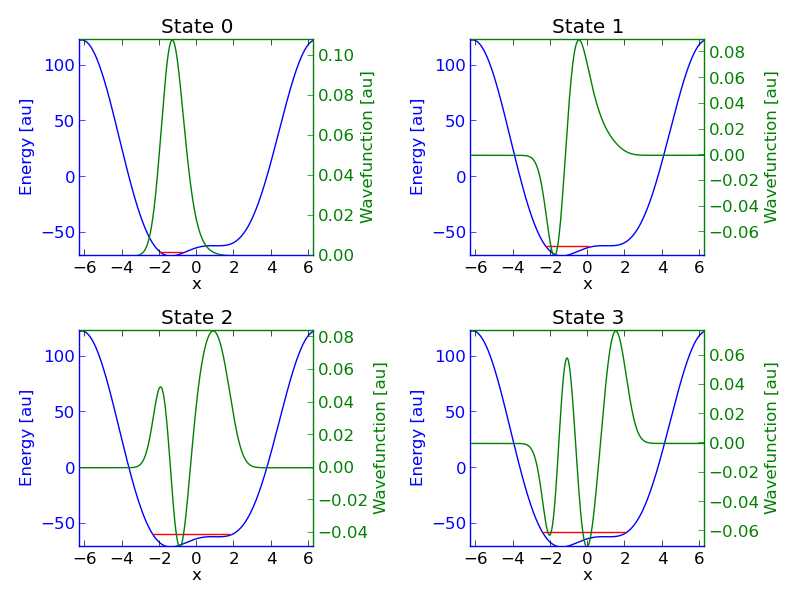
The algorithm itself was pretty straightforward:
And before you know it, you’ve solved the problem!
There were a couple computational tricks that came in handy, such as using SciPy’s sparse matrix library to reduce the complexity of the problem from quadratic to linear in the number of discretized chunks. Nonetheless, the process of creating this was fast (roughly a day’s work) and incredibly illuminating, so much so that I feel an assignment like this should be included in any quantum class for physics majors.
As demonstrated by PhET, students can gain a great deal of intuition from simple simulations. I’ll keep expanding on, testing, and generalizing this software before I make it available, but, in the meantime, it’s got some nice results. Time to go run some measurements and see how it works! I expect the spectroscopy to show something like this for our qubit transitions: